<맨 위로>

2강. 원자 오비탈 & 결합
- 슈뢰딩거 방정식 - 수소꼴 원자

2강. 원자 오비탈 & 결합

슈뢰딩거 방정식 - 수소꼴 원자

지난 시간에 1차원 상자 속 입자에 대하여 슈뢰딩거 방정식을 풀어보았다. 수소꼴 원자에서 슈뢰딩거 방정식은 아래와 같다.

\[-\frac{\hslash^2}{2m}\nabla^2 \psi - \frac{Ze^2}{4\pi \epsilon_0 r}\psi = E\psi\] \[\nabla^2=\frac{1}{r^2}\frac{\partial}{\partial r}\left( r^2 \frac{\partial}{\partial r} \right)+\frac{1}{r^2 \sin \theta}\frac{\partial}{\partial \theta}\left( \sin \theta \frac{\partial}{\partial \theta}\right)+\frac{1}{r^2\sin^2 \theta}{\partial^2}{\partial \phi^2}\]

이 방정식을 푸는 것은 생략한다. 우리는 결과만 배우고 넘어가자.

상자 속 입자에서는 방정식을 풀었을 때 $n$이 등장하였다. 비슷하게 수소꼴 원자에서 방정식을 풀면 $n, l, m_l$이 등장한다.

상자 속 입자에서 $n$의 조건은 $n \in \mathbb{N}$이였다. 수소꼴 원자에서 $n, l, m_l$의 조건은 다음과 같다.

\[n \in \mathbb{N}\] \[l \in \{0, 1, \ldots, n-1\}\] \[m_l \in \{0, \pm 1, \ldots, \pm l \}\]

위 조건은 만족하도록 $n, l, m_l$을 정해주면 파동함수와 에너지가 정해진다.

오비탈이란, 원자핵에 구속되어 있는 1 전자 파동함수를 의미한다. $n$과 $l$을 이용해 오비탈의 이름을 붙이는데, $l=0, 1, 2, 3$일 때 각각 알파벳 $s, p, d, f$를 붙인다.

예를 들어 $n=1, l=0$인 파동함수는 $1s$ 오비탈이고, $n=3, l=1$인 파동함수는 $3p$ 오비탈이다.

여기서 주의할 점은, $n=2, l=1$인 $2p$오비탈에서 $m_l$이 $+1, 0, -1$인 것이 각각 $2p_x, 2p_y, 2p_z$에 대응하는 것이 아니라는 것이다. 일반적으로 슈뢰딩거 방정식을 풀었을 때는 복소함수가 나오게 되고, 이를 실함수로 바꾸기 위해 $2p_x$는 $m_l=+1$인 것과 $m_l=-1$인 것을 더해서 만들고, $2p_y$는 $m_l=+1$인 것과 $m_1=-1$인 것을 빼서 만든다. $2p_z$는 $m_l=0$인 것에 해당한다.

수소꼴 원자의 파동함수는 $\psi=R \times Y$로 쓸 수 있고, $R$은 $n, l$에 따라 결정되는 함수, $Y$는 $l, m_l$에 따라 결정되는 방향에만 의존하는 함수이다.

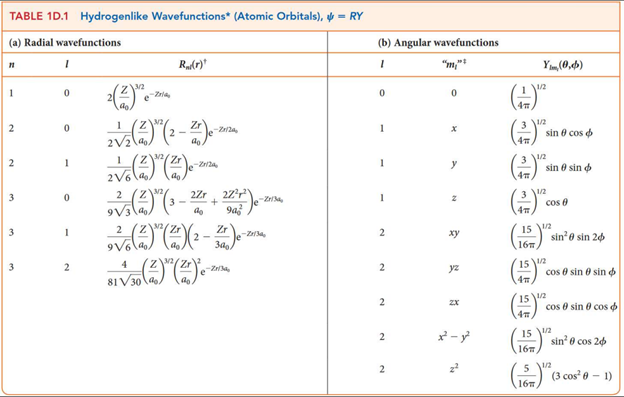
예를 들어 $\psi_{2p_x}=\frac{1}{4\sqrt{2\pi}}\left(\frac{Z}{a_0}\right)^{\frac{3}{2}}\left(\frac{Zr}{a_0}\right)e^{-\frac{Zr}{a_0}}\sin \theta \cos \varphi$인데, 이는 너무 복잡하게 생겼다. 그래서 오비탈을 한 눈에 알아보기 쉽도록 이 함수의 같은 함숫값을 갖는 점들의 집합(등위면)으로 나타낸다. 파동함수의 부호가 반전되는 지점을 마디(nodal plane)이라 부른다.

원자 오비탈 그림

원자 오비탈의 그림은 다음과 같이 생겼다.

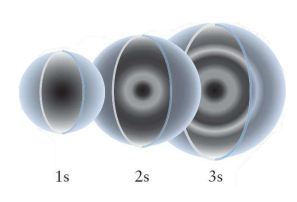
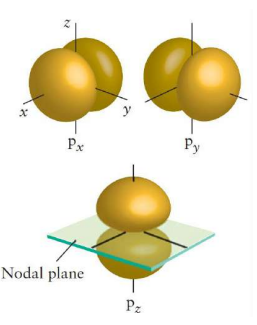
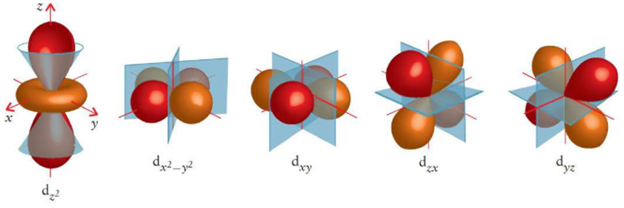
마디는 다음 두 가지 종류로 나뉜다.

방사상 마디: 원점을 포함하지 않는 구형 마디, $n-l-1$개
각상 마디: 원점을 포함하는 마디, $l$개

원자 오비탈 에너지 준위

수소꼴 원자에서는 $E=-\frac{Z^2}{n^2}R_H$로, 에너지 준위가 $n$값에만 의존한다.

여기서 다른 오비탈이 같은 에너지 준위를 갖는 현상을 축퇴(degenerate)라고 한다. 수소꼴 원자에서는 $2s$ 오비탈과 $2p$ 오비탈이 축퇴되어있다고 말할 수 있다.

다전자 원자에서는 슈뢰딩거 방정식을 엄밀히 푸는 것이 불가능하다(3체 문제). 그래서 수소꼴을 기준으로, 각종 근사를 적용한다.

가리움 효과

먼저, 다음 두 가지 확률을 구분할 필요가 있다.

특정 지점에서의 발견 확률: $\psi^2$
핵에서부터 특정 거리에서의 발견 확률: $4\pi r^2 \times \psi^2$
상수를 제외하고 $r^2\psi^2$으로 쓰거나, $\psi=R \times Y$에서 $Y$는 방향에만 의존하므로 $r^2R^2$로 쓰기도 한다.

$2s$ 오비탈에서 $\psi^2$와 $r^2\psi^2$의 그래프는 아래와 같다.

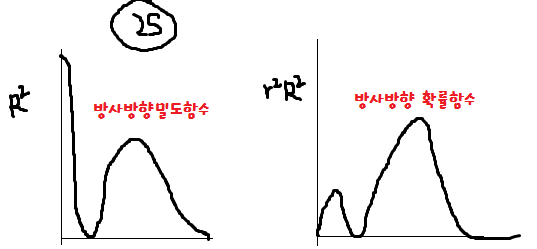
아래 그래프는 $2s$ 오비탈과 $2p$ 오비탈의 방사방향 확률분포 그래프이다.

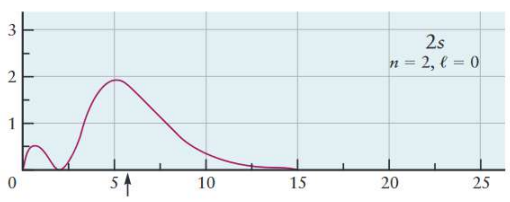
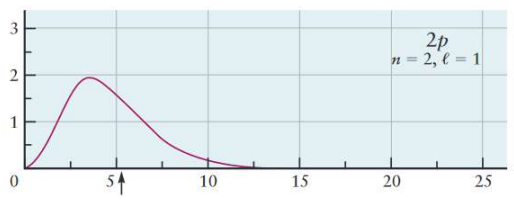
화살표로 표시된 부분이 전자가 발견되는 평균 거리이다.

전자가 발견되는 평균 거리: $2s > 2p$
But, 전자가 핵에서 매우 가깝게(=$1s$보다 가깝게) 발견될 확률: $2s>2p$
$\implies$ $1s$ 오비탈을 뚫고 핵으로 당겨질 확률: $2s>2p$
$\implies$ 가리움 효과의 크기: $2s<2p$ $\implies$ 다전자 에너지 준위: $2s<2p$

이를 두고 $2s$ 오비탈이 $2p$ 오비탈보다 침투효과가 크다라고 말한다.

요약해서 다전자 원자에서 오비탈의 에너지 준위는 아래 그림과 같다.

가리움 효과 추정법: Slater 규칙

우선 $n$ 순서대로 전자들을 묶음. 단, s와 p는 같은 그룹 $$[1s][2s, 2p][3s, 3p][3d][4s, 4p]\cdots$$
같은 그룹끼리는 0.35만큼 가림. 단, $[1s]$ 그룹 한정 0.30
$[ns, np]$ 그룹은 $(n-1)$ 그룹에 의해 0.85 가려짐. $(n-2)$ 이하 그룹에 의해 1씩 가려짐.
$[nd]$나 $[nf]$ 그룹은 자기 이하의 그룹에 의해 1씩 가려짐

위 규칙을 적용해서 $Mg$의 최외각 전자가 느끼는 유효 핵전하를 구해보자.

$Mg$의 오비탈은 $1s^22s^22p^63s^2$이다. 그룹으로 묶어보면 $\underbrace{[1s]}_{2개}\underbrace{[2s, 2p]}_{8개}\underbrace{[3s]}_{2개}$이다.
최외각 전자는 $3s$ 오비탈에 존재하므로, 같은 그룹에 있는 전자 1개에 의한 가리움 효과는 $0.35 \times 1$
$(n-1)$ 그룹에 있는 전자 8개에 의한 가리움 효과는 $0.85 \times 8$
$(n-2)$ 이하 그룹에 있는 전자 2개에 의한 가리움 효과는 $1 \times 2$

$Fe$의 최외각 전자에 대해서도 적용해보자.

$Fe$의 오비탈은 $1s^22s^22p^63s^23p^64s^23d^6$이다. 그룹으로 묶어보면 $$\underbrace{[1s]}_{2개}\underbrace{[2s, 2p]}_{8개}\underbrace{[3s, 3p]}_{8}\underbrace{[3d]}_{6}\underbrace{[4s]}_{2}$$이다.
최외각 전자는 $4s$ 오비탈에 존재하므로, 같은 그룹에 있는 전자 1개에 의한 가리움 효과는 $0.35 \times 1$
$(n-1)$ 그룹에 있는 전자 14개에 의한 가리움 효과는 $0.85 \times 14$
$(n-2)$ 이하 그룹에 있는 전자 10개에 의한 가리움 효과는 $1 \times 10$

$Fe$의 $3d$ 오비탈에 있는 전자가 느끼는 유효핵전하를 구해보면

같은 그룹에 있는 전자 5개에 의한 가리움 효과는 $0.35 \times 5$
자기 이하 그룹에 있는 전자 18개에 의한 가리움 효과는 $1 \times 18$

전자 스핀: Stern-Gerlach 실험

전자는 다음 두 가지 스핀이 존재한다.

왼쪽 그림은 up 스핀 또는 $\alpha$ 스핀이라고 부르고, 스핀 양자수 $m_s=+\frac{1}{2}$이다. 위쪽이 자석의 $S$극에 해당한다. 오른쪽 그림은 down 스핀 또는 $\beta$ 스핀이라고 부르고, $m_s=-\frac{1}{2}$이다. 위쪽이 자석의 $N$극에 해당한다.

전자의 스핀으로 인해 원자 빔을 자기장에 통과시키면 두 갈래로 나뉘게 된다.

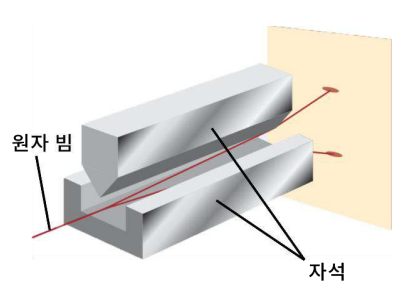
이때 사용하는 원자는 홀전자가 있는 원자여야 한다. (${}1\operatorname{H}, {}{47}\operatorname{Ag}$ 등)

다전자 원자에서 전자 채우기

다전자 원자에서 전자를 채울 때, 다음 세 가지 규칙을 만족해야 한다.

Pauli 배타 원리: 모든 전자의 양자수는 서로 다르다.
Aufbau 원리(쌓음 원리): 에너지가 낮은 오비탈부터 채운다.
Hund 규칙: $\Sigma m_s$가 최대인 상태가 가장 에너지가 낮다.

${}_{8}\operatorname{O}, {}_{8}\operatorname{O}^{2+}$ 전자 채우기
${}_{11}\operatorname{Na}, {}_{11}\operatorname{Na}^+$ 전자 채우기
${}_{26}\operatorname{Fe}, {}_{26}\operatorname{Fe}^{2+}$ 전자 채우기
${}_{29}\operatorname{Cu}, {}_{29}\operatorname{Cu}^+$ 전자 채우기
${}_{24}\operatorname{Cr}, {}_{24}\operatorname{Cr}^{3+}$ 전자 채우기